

Bei Schrägbilddarstellungen von räumlichen Körper lassen wir uns leicht täuschen. Im Vergleich zur ebenen Geometrie im \(R^2\), bei der wir nur zwischen den Betrachtung von "links oder rechts" sowie "oben oder unten" unterscheiden müssen, kommt im \(R^3\) die Unterscheidung der Blickrichtung von "vorne oder hinten" hinzu.
In diesem Kapitel werden wir zunächst ein mögliches Koordinatensystem des \(R^3\) einführen und mit diesem die Lage von geometrischen Objekten im Raum beschreiben.
| Für das Zeichnen von räumlichen Koordinatensystemen hat sich das
Verfahren der
Schrägbilddarstellung bewährt: Dazu wird die \(x_1\)-Achse vom Ursprung aus unter \(45°\) nach links unten gezeichnet. Die Einheiten auf der \(x_2\)- und \(x_3\)-Achse betragen jeweils \(1 \space cm\) und auf der \(x_1\)-Achse ist die Einheit eine Kästchendiagonale. |
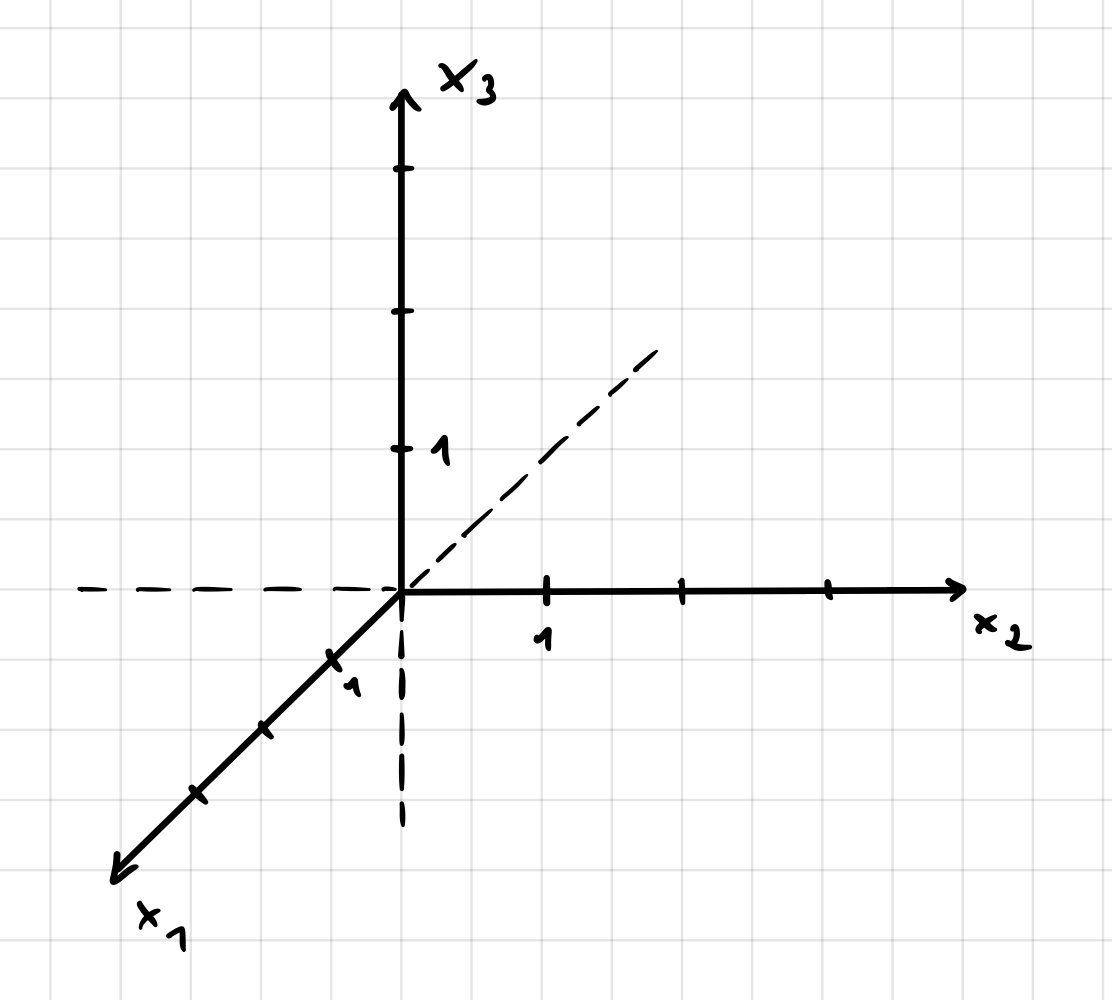 |
| Bei dieser Darstellungsform ergeben sich zwar etwas
verzerrte Bilder, die aber einfach zu realisieren sind und zudem
ausreichend realistisch wirken. Andere Formen der Darstellung wären Normalbilder in Isomerie, Dimetrie oder Trimetrie. Alle drei Formen zeigen Figuren so, wie wir sie aus großer Entfernung wirklich sehen. Die zugehörigen Koordinatensysteme werden nach speziellen Regeln aufgestellt, sind aber deutlich schwieriger zu realisieren und werden daher im Schulunterricht kaum verwendet. Bei Interesse: Axonometrie auf Wikipedia |
|
Anwendung des Applets: