Vektoren sind keineswegs an einem bestimmten Punkt fixiert, sondern Pfeile, die eine eindeutig festgelegte Verschiebung veranschaulichen, die mit jedem beliebigen Punkt des Raumes durchgeführt werden kann.
Eine Addition von Vektoren kann also als zwei oder mehreren Verschiebungen aufgefasst werden, die von einem Startpunkt hintereinander ausgeführt werden.
Praktisch addieren wir zwei Vektoren \(u\) und \(v\), indem wir sie aneinanderhängen. Der Fuß des zweiten Vektors (zweite Verschiebung) wird an die Spitze des ersten Vektors (erste Verschiebung) gesetzt.
Das Ergebnis der Vektoraddition ist der Summenvektor \(u+v\), der das Ergebnis der zweifachen Verschiebung als Gesamtverschiebung darstellt.
Beispiel:
Der Punkt \(P(1|1|1)\) wird zuerst mit dem
Vektor \( \vec{u} = \left( \begin{array}{c} 2 \\ 4 \\ 1 \end{array}\right) \)
und anschließend mit dem Vektor \( \vec{v} = \left( \begin{array}{c}
-5 \\ 2 \\ 3 \end{array} \right) \) verschoben.
Wir erhalten die Gesamtverschiebung: \( \hspace{10mm} \vec{u}+\vec{v} = \left( \begin{array}{c} -3 \\ 6 \\ 4 \end{array} \right) \).
| Verschiebung im Schrägbild | Verschiebung dreidimansional | |
 |
 |
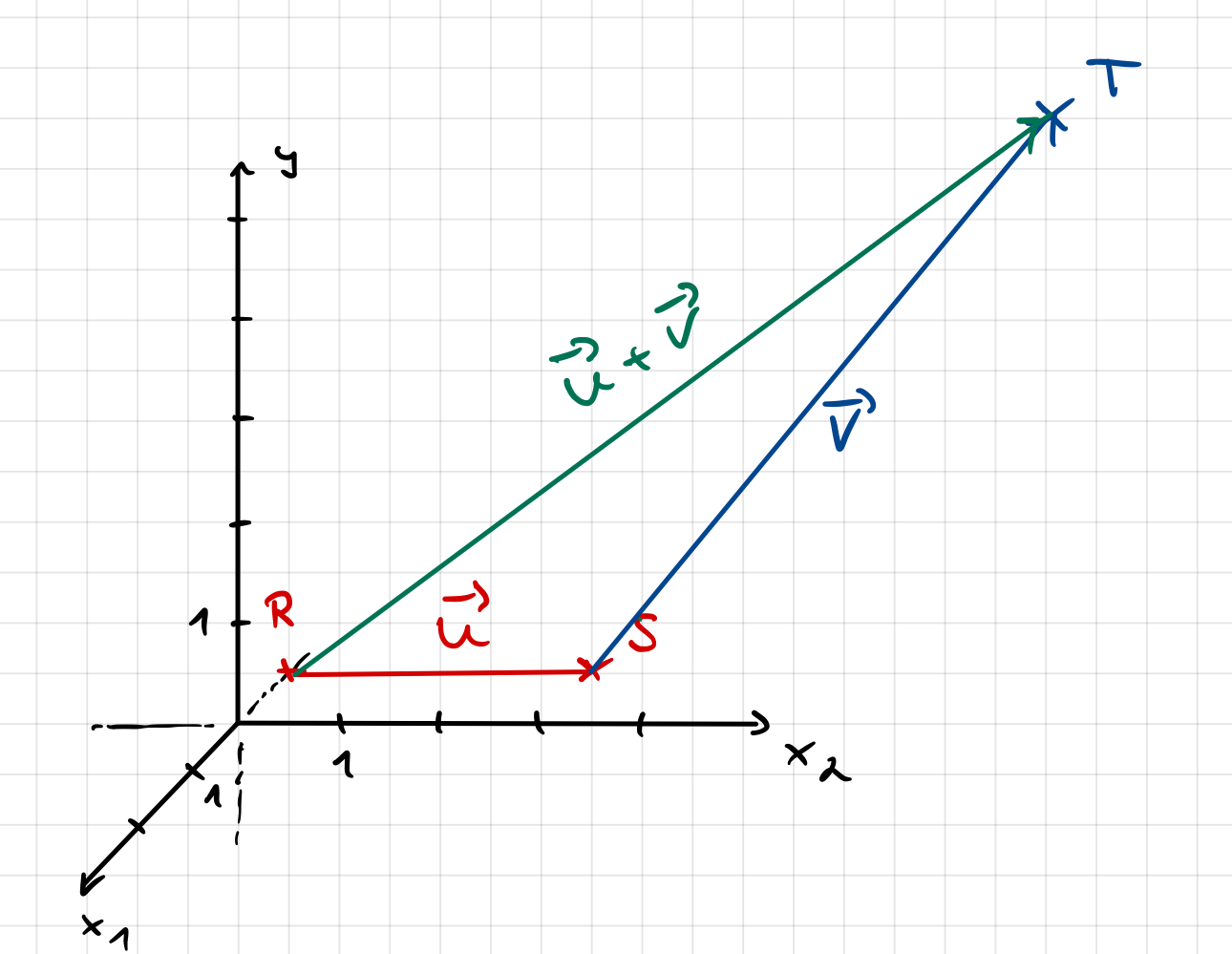Vektoren werden entsprechend der Umsetzung im Schrägbild koordinatenweise addiert.
Die erste Koordinate des ersten Vektors wird mit der ersten Koordinate des zweiten Vektors addiert. Danach kommt die zweite Koordinaten entsprechend an die Reihe und am Ende die dritte.
Im Beispiel:
Verschiebungen mit Vektor \( \vec{u} = \left( \begin{array}{c} 2 \\ 4 \\ 1 \end{array}\right) \) und und dem dem Vektor \( \vec{v} = \left( \begin{array}{c} -5 \\ 2 \\ 3 \end{array} \right) \)
ergibt: \( \vec{u}+\vec{v}= \left( \begin{array}{c} 2 \\ 4 \\ 1 \end{array}\right) + \left( \begin{array}{c} -5 \\ 2 \\ 3 \end{array} \right) = \left( \begin{array}{c} 2+(-5) \\ 4+2 \\ 1+3 \end{array} \right) = \left( \begin{array}{c} -3 \\ 6 \\ 4 \end{array} \right) \)
Der Punkt \(P(1|1|1)\) wird als insgesamt verschoben mit dem Vektor \( \left( \begin{array}{c} -3 \\ 6 \\ 4 \end{array} \right) \)
|
Ergebnis: Rechnerisch erhalten wir den Summenvektor \( \vec{u} + \vec{v}\) in dem wir die Vektoren koordinatenweise addieren: \[ \vec{u}+\vec{v}= \left( \begin{array}{c} u_1 \\ u_2 \\ u_3 \end{array}\right) + \left( \begin{array}{c} v_1 \\ v_2 \\ v_3 \end{array} \right) = \left( \begin{array}{c} u_1+v_1 \\ u_2+v_2 \\ u_3+v_3 \end{array} \right) \]
|
5.1 Vektoraddition
Anschaulich
erhalten wir den Summenvektor \( \vec{u}+ \vec{v} \) der
Addition zwei beliebiger Vektoren \( \vec{u}\) und \( \vec{v} \),
indem wir den Fuß des Vektors \( \vec{v} \) an die Spitze des
Vektors \( \vec{u} \) anfügen.