3.2.2 Ebenengleichung durch eine Gerade und einen Punkt

Sind eine Gerade \(g\) und ein Punkt \(P\) gegeben und der Punkt \(P\) liegt nicht auf der Geraden, dann können wir durch diese beiden Objekte eindeutig eine Ebene aufstellen.

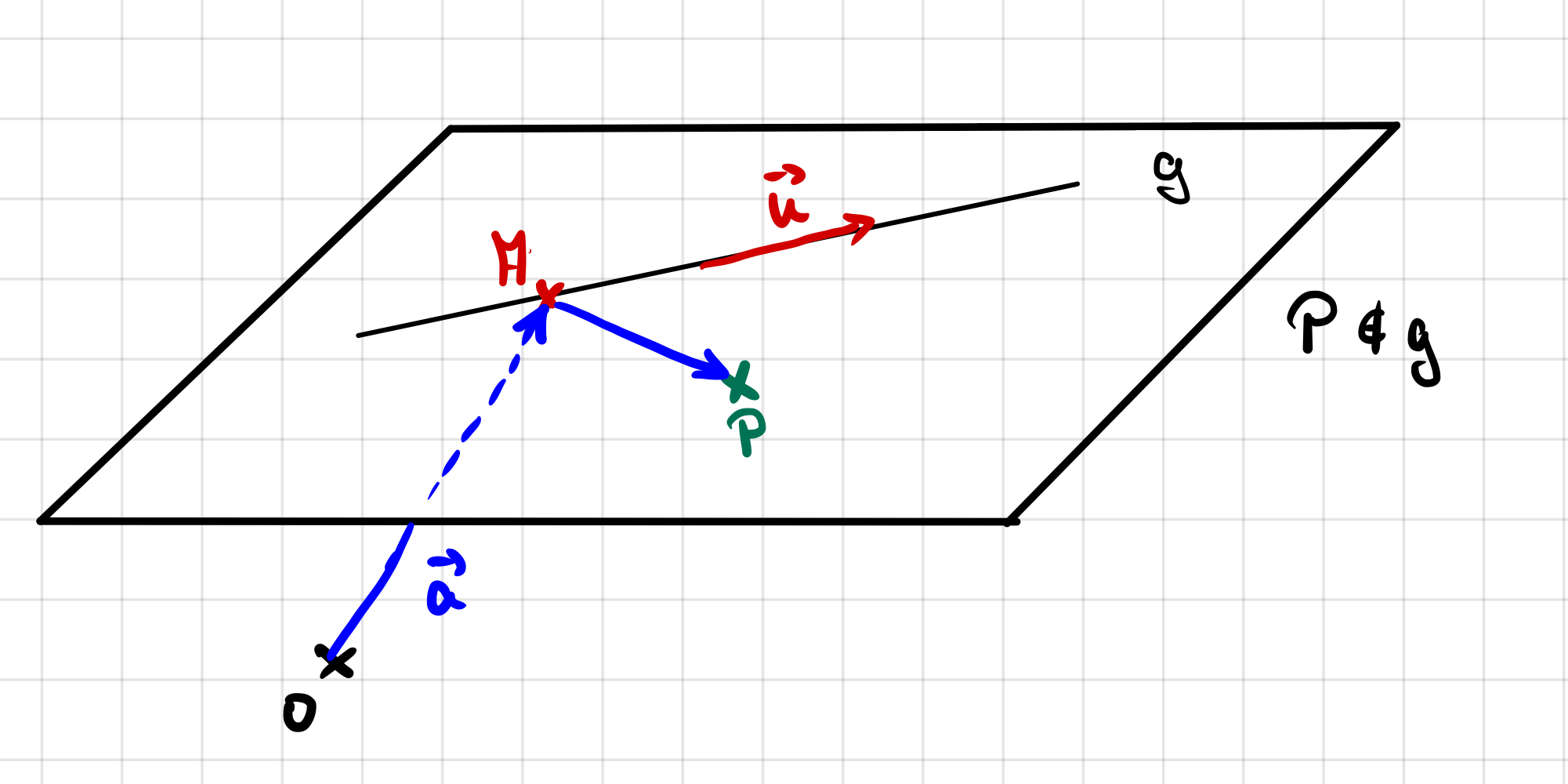
\(PF(E): \vec{X}=\vec{a}+\lambda \cdot \vec{u} + \mu \cdot \vec{AP} \)

• Die Gerade liefert den Aufpunkt \(A\) der Ebene
• und einen Richtungsvektor \(\vec{u}\).
• Der Vektor \(\vec{AP}\) ist der zweite Richtungsvektor der gesuchten Ebene \(E\).