3.2.3 Ebenengleichung aus zwei Geraden

Sind zwei Geraden gegeben, die sich entweder schneiden oder echt parallel verlaufen, dann können wir ebenfalls sehr schnell eine Ebenengleichung der Ebene \(E\) in Parameterform festlegen, in der die beiden Geraden liegen.

 

Die Geraden schneiden sich

Falls die Richtungsvektoren zweier Geraden keine Vielfachen voneinander sind,

muss überprüft werden, ob sich die Geraden schneiden. Falls ja, nimmt man beispielsweise den Schnittpunkt \(S\) als Aufpunkt und die Richtungsvektoren beider Geraden als Richtungsvektoren der Ebene.   Die Aufpunkte der Geraden wären ebenfalls als Aufpunkt der Ebene möglich!

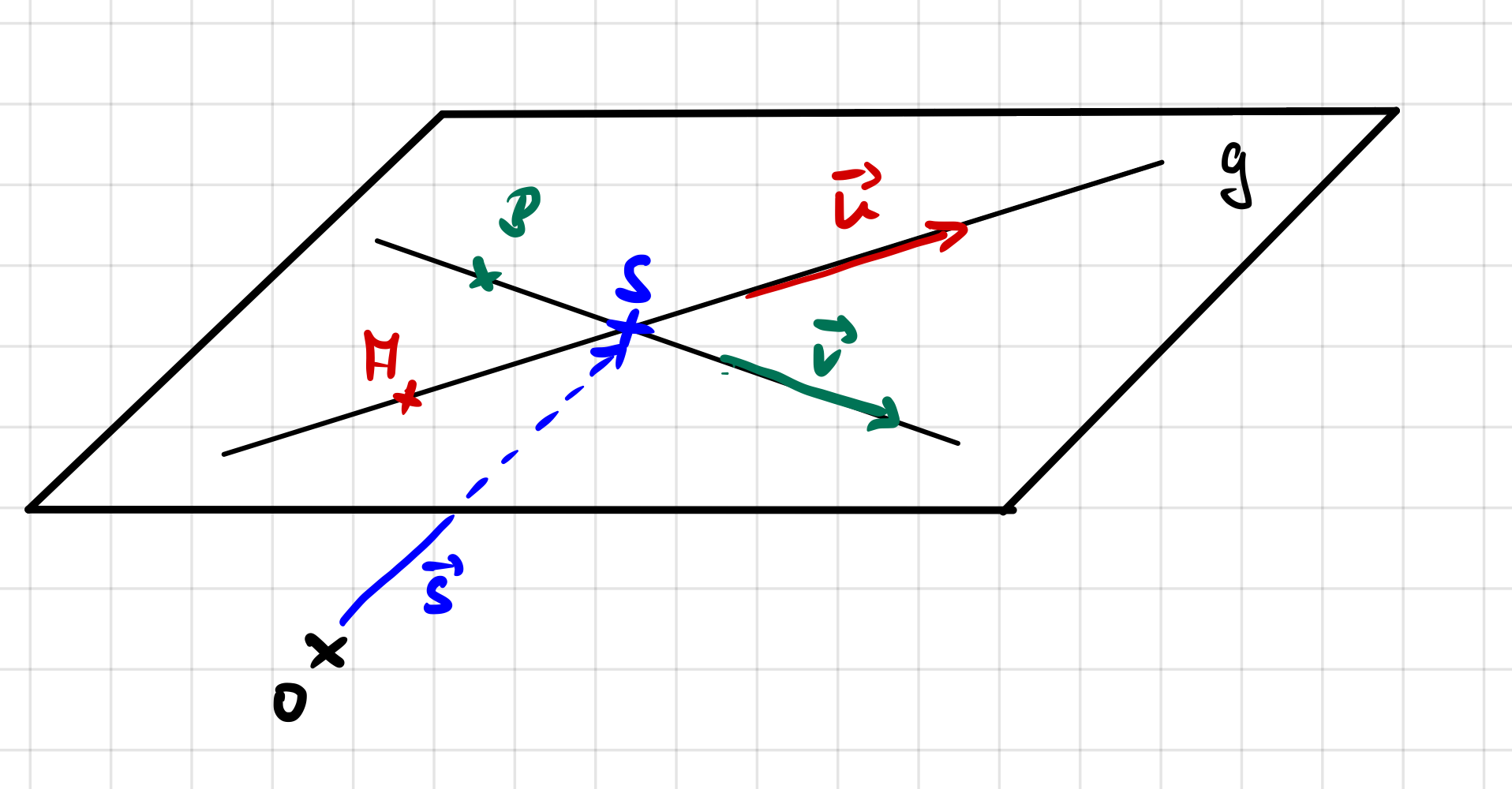
\(PF(E): \vec{X}=\vec{s}+\lambda \cdot \vec{u} + \mu \cdot \vec{v} \)

 

Beispiel:

 

Die Geraden sind parallel

Falls die Richtungsvektoren zweier Geraden Vielfache voneinander sind

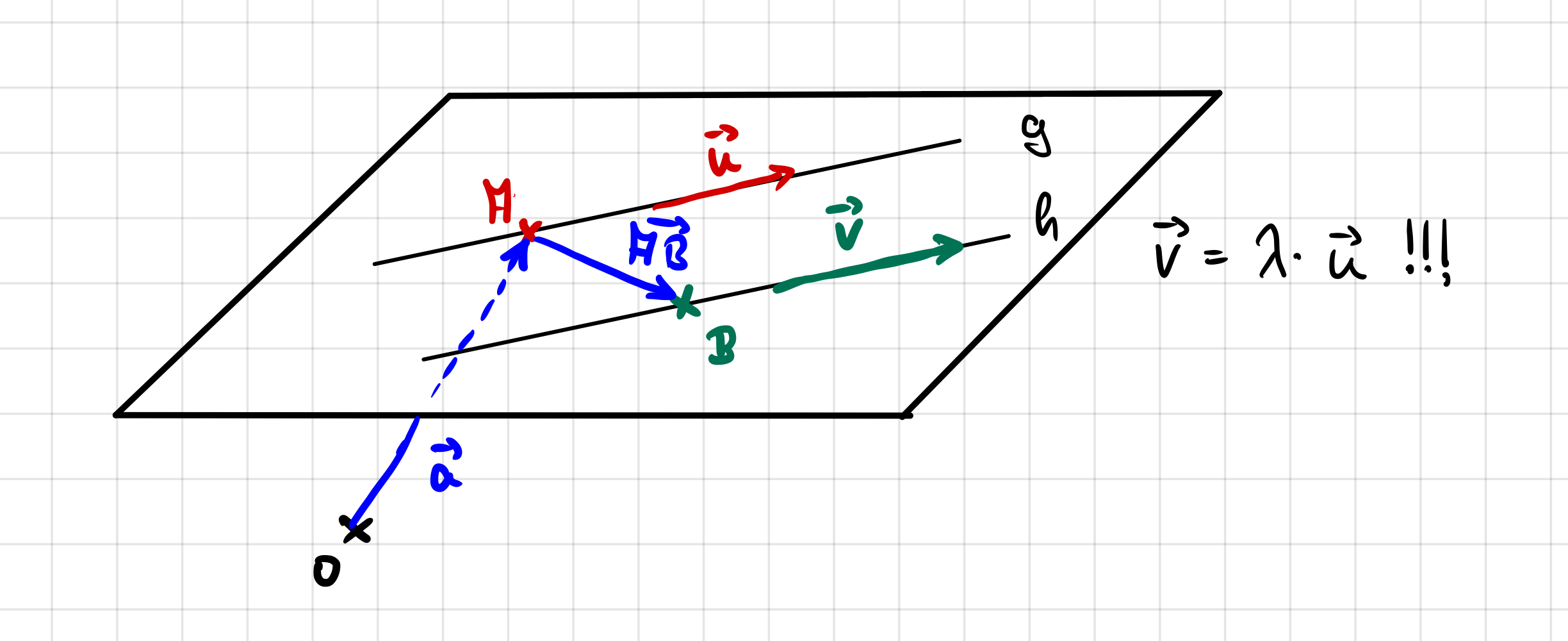
	\(PF(E): \vec{X}=\vec{a}+\lambda \cdot \vec{u} + \mu \cdot \vec{AB} \)
muss überprüft werden, ob der Aufpunkt der einen Geraden auf der anderen Geraden liegt. Falls nicht, dann sind die Geraden echt parallel. Der Richtungsvektor einer Geraden und der Verbindungsvektor ihrer Aufpunkte bilden die Richtungsvektoren der Ebene. Einer der beiden Aufpunkte der Geraden wird als Aufpunkt der Ebene festgelegt!

Beispiel:

 

 

---