Bild_Oben

3.4.1.2 Abstand eines Punktes von einer Geraden

Liegt ein Punkt P nicht auf einer Geraden g, dann müssen wir häufig dessen Abstand von der Geraden bestimmen.

 

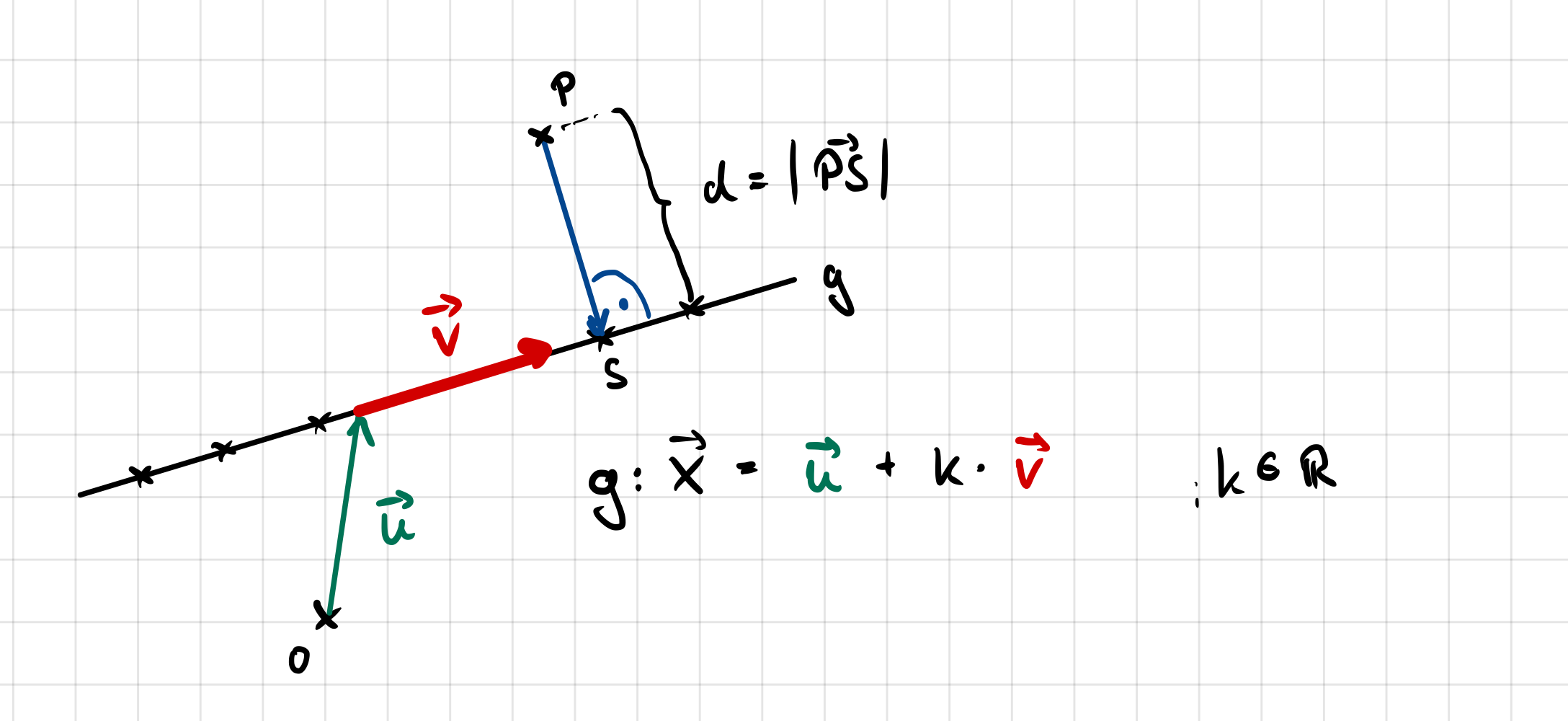
Grundlagen der Abstandsbestimmung:

  • Abstände werden immer im rechten Winkel gemessen.
  • Wir bestimmen also einen Punkt S auf der Geraden g so, dass die Strecke \( [PS] \) senkrecht zur Geraden g steht.
  • Die Länge der Strecke \( [PS] \) gibt den Abstand d.

  

Abstandsbestimmung mit dem allgemeinen Geradenpunkt

In der Vektorgeometrie bedeuten diese Grundlagen, dass

  • unser Vektor \(\small \vec{PS} \) senkrecht zur Geraden g verläuft:  \(\small \vec{PS} \perp g\)
  • und damit \(\small \vec{PS} \) senkrecht zum Richtungsvektor \( \small \vec{v}\) verlaufen muss: \(\small \vec{PS} \perp \vec{v}\)
  • Der Punkt S ist ein noch unbekannter Punkt auf der Geraden, der sich durch einen noch zu bestimmenden Wert k ergibt.
  • Der Trick der weiteren Berechnung ist die Umformung der Geradengleichung zum  allgemeinen Geradenpunkt der Geraden:

     \(\vec{X}=\vec{u}+k \cdot \vec{v} = \left( \begin{array}{c} u_1  \\ u_2 \\ u_3  \end{array}\right) + k \cdot  \left( \begin{array}{c} v_1 \\ v_2 \\ v_3  \end{array}\right)=\left( \begin{array}{c} u_1+k \cdot v_1  \\ u_2 + k \cdot v_2\\ u_3 + k \cdot v_3  \end{array}\right)  \)

    Anschaulich: Jeder Wert k bestimmt sofort den Ortsvektor zu einem Punkt!

 

Abstand und allgemeiner Geradenpunkt im Beispiel

Gegeben ist der Punkt \(A(1|6|4) \) und die Gerade g:   \( \small \vec{X}= \left( \begin{array}{c} 1  \\ -2 \\ 2  \end{array}\right) + k \cdot  \left( \begin{array}{c} -1 \\ 3 \\ 2  \end{array}\right)\)

Bestimme den Abstand des Punkte A von der Geraden g!

 

 

Gesucht ist ein noch unbekannter Punkt S auf der Geraden, für den der Vektor \(\small \vec{AS} \) senkrecht zur Geraden g bzw. der Richtungsvektor \(\vec{v}\) steht.
Der allgemeine Geradenpunkt S: \(\vec{S}=\left( \begin{array}{c} 1-k  \\ -2 + 3 k\\ 2 + 2  k  \end{array}\right)  \)
Damit ergibt sich:  \(\hspace{5mm} \color{red}{\vec{AS}} \perp \vec{v} = 0 \hspace{5mm} \Leftrightarrow \) \(\space \Biggl \lbrack    \left( \begin{array}{c} 1-k  \\ -2 + 3 k\\ 2 + 2  k  \end{array}\right) -  \left( \begin{array}{c} 1 \\ 6 \\ 4  \end{array}\right) \Biggr \rbrack  \circ  \left( \begin{array}{c} -1 \\ 3 \\ 2  \end{array}\right)=0 \)
Dabei ist: \( \space \color{red}  {\vec{AS}= \left( \begin{array}{c} -k  \\ -8 + 3 k\\ -2 + 2  k  \end{array}\right)}\) \( \space \color{red}  { \left( \begin{array}{c} -k  \\ -8 + 3 k\\ -2 + 2  k  \end{array}\right)}  \circ  \left( \begin{array}{c} -1  \\ 3\\ 2  \end{array}\right)=0\)
\(\space k-25+9k-4+4k=0 \hspace{2mm} \Rightarrow \hspace{2mm} \color{red}{k=2}\)

    

Der Abstand des Punktes A von der Geraden g ergibt sich mit \(k=2\) durch
den Betrag des Vektors \(\vec{AS}\):

\( d= |\vec{AS}| = \Biggl | { \left( \begin{array}{c} -2  \\ -2\\  2    \end{array}\right)} \Biggr |  = \sqrt{(-2)^2+(-2)^2+2^2}=\sqrt{12}=2\sqrt{3}\)