4.4 Lagebeziehung zwischen Gerade und Ebene

Bei der Untersuchung der verschiedenen Lagen einer Gerade bzgl. einer Ebene treffen wir auf folgende drei Möglichkeiten:

 

Gerade g verläuft echt parallel zur Ebene E	Gerade g und Ebene E schneiden sich in einem Punkt S	Gerade g verläuft in der Ebene E
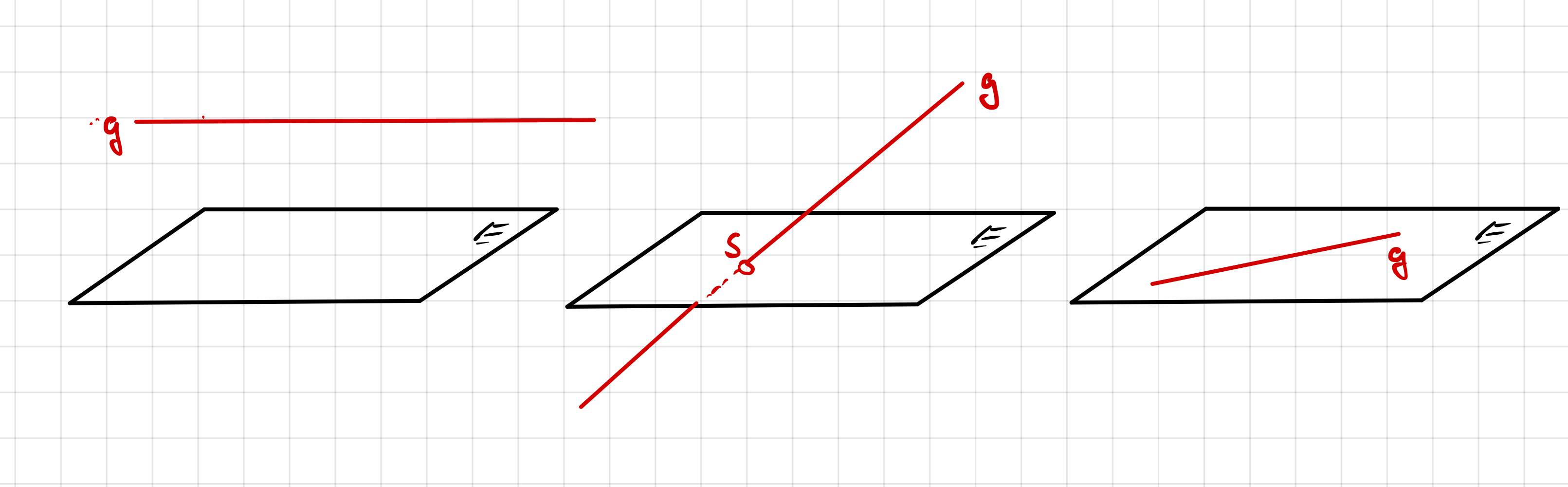Es existiert kein gemeinsamer Punkt.	Es existiert genau ein gemeinsamer Punkt.	Es existieren unendlich viele gemeinsame Punkte.

 

Verschiedene Strategien zur Untersuchung

Grundsätzlich gibt es zwei unterschiedliche Vorgehensweisen, mit denen wir die Lage der beiden Objekte zueinander eindeutig bestimmen können.

Variante 1:	- Allgemeinen Geradenpunkt bestimmen - Punktprobe mit Ebene - Ergebnis der Gleichung deuten
Variante 2:	- Lage vom Richtungsvektor zum Normalenvektor deuten - entweder Punktprobe mit Aufpunkt der Geraden - oder Punktprobe mit allgemeinen Geradenpunkt

Die Bestimmung der gegenseitigen Lagebeziehung kann mit allen drei gängigen Ebenenformen erfolgen, jedoch hat die Koordinatenform der Ebene in diesem Fall große Vorteile.

  

---