4.4.3 Lageuntersuchung mit Normalen- und Richtungsvektor

Die gegenseitige Lage von Gerade und Ebene kann durch die Betrachtung der Richtung vom Normalenvektor \(\vec{n}\) der Ebene im Vergleich zum Richtungsvektor \(\vec{u}\) der Geraden erfolgen. Liegt die Ebene in Parameterform vor, muss für diesen Weg also erst der Normalenvektor bestimmt werden.

Für die Einordnung der Lagebeziehung ist grundlegend entscheidend, ob Normalen- und Richtungsvektor senkrecht aufeinander stehen.

 

\(\vec{u} \circ \vec{n} = 0\)  und der Aufpunkt  A der Geraden g liegt nicht in E	\(\vec{u} \circ \vec{n} \neq 0\)	\(\vec{u} \circ \vec{n} = 0\)  und der Aufpunkt  A der Geraden g liegt in E
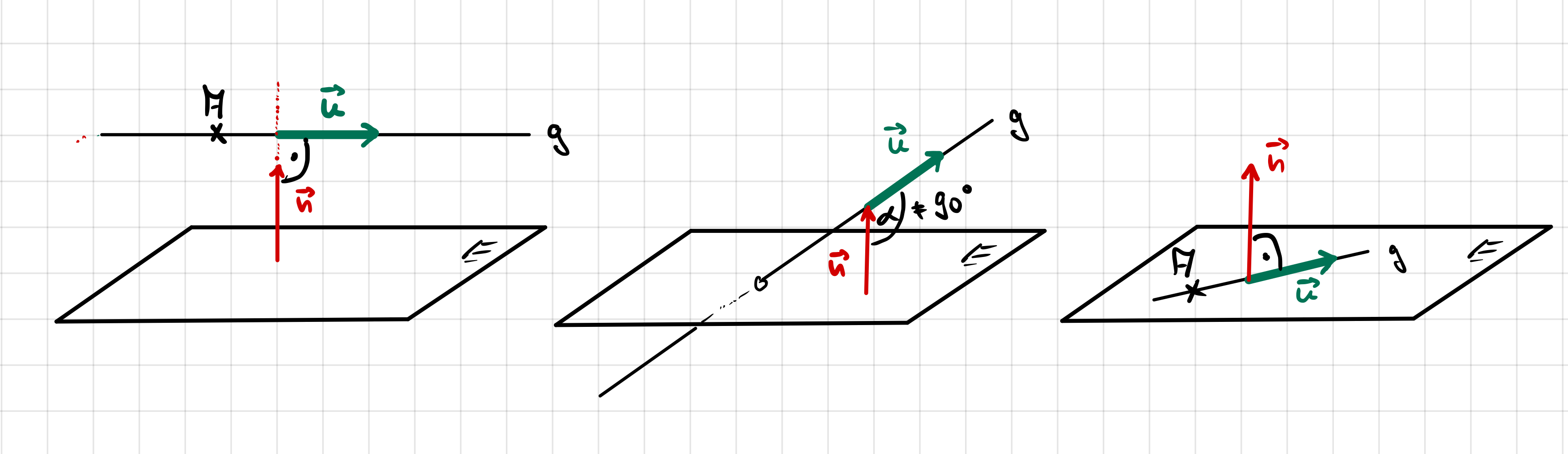g verläuft parallel zu E	g und E schneiden sich	g liegt in E

 

Lagebeziehung zwischen Gerade und Ebene

• Falls  \(\vec{n}\)    \(\vec{u} \space \Leftrightarrow  \space \vec{n} \circ \vec{u} \neq 0\)
  
  \( \Rightarrow\)   g und h scheiden sich in genau einem Punkt
  \( \Rightarrow\)  Schnittpunkt S wird über Methode allgemeiner Geradenpunkt berechnet.
   
   
• Falls  \(\vec{n}  \perp  \vec{u} \space \Leftrightarrow  \space \vec{n} \circ \vec{u} = 0\)
  
  \( \Rightarrow\) Prüfe, ob Aufpunkt A der Geraden in der Ebene liegt.
     -> Falls A in E liegt, dann verläuft die gesamte Gerade g in der Ebene E.
     -> Falls A nicht in E liegt, dann sind die Gerade g und die Ebene echt parallel.
  

 

Beispiel zur Lagebeziehung

Gegeben sind die Ebene E:  \(4x_1+x_2-2x_3-6=0\)

und die Gerade  \(\small g: \space \vec{X}=\left( \begin{array}{c} -2 \\ 3 \\ 4  \end{array}\right)  + k \cdot  \left( \begin{array}{c} 1 \\ 4 \\ 4  \end{array}\right)   \) 

 

Schritt 1: Wir untersuchen das Skalarprodukt aus Normalenvektor und Richtungsvektor:

\(\small \vec{n} \circ \vec{u}=\left( \begin{array}{c} 4 \\ 1 \\ -2  \end{array}\right) \circ  \left( \begin{array}{c} 1 \\ 4 \\ 4  \end{array}\right)   = 4 \cdot 1 + 1 \cdot 4 + (-2) \cdot 4 = 0 \)

D.h. entweder verläuft g in  E oder g ist echt parallel zu E
 

Schritt 2: Wir prüfen, ober der Aufpunkt \(A(-2|3|4) \) der Geraden g in der Ebene E liegt:

Punktprobe mit E:   \(4 \cdot (-2) + 3 -2 \cdot 4 - 6 \neq 0 \)

D.h. der Aufpunkt A liegt nicht in E. g und E sind somit echt parallel!

 

---