Bild_Oben

4.4.1 Methode - Allgemeiner Geradenpunkt mit KF(E)

Liegt die Ebene in Koordinatenform vor, so können wir mit Hilfe des allgemeinen Geradenpunktes sehr effektiv die jeweilige Lagebeziehung angeben:

  • Bestimme den allgemeinen Geradenpunkt der Geradengleichung
  • und setzte diesen in die Gleichung der Ebene ein.
  • Die Gleichung hat entweder keine, genau eine oder unendlich viele Lösungen.

 

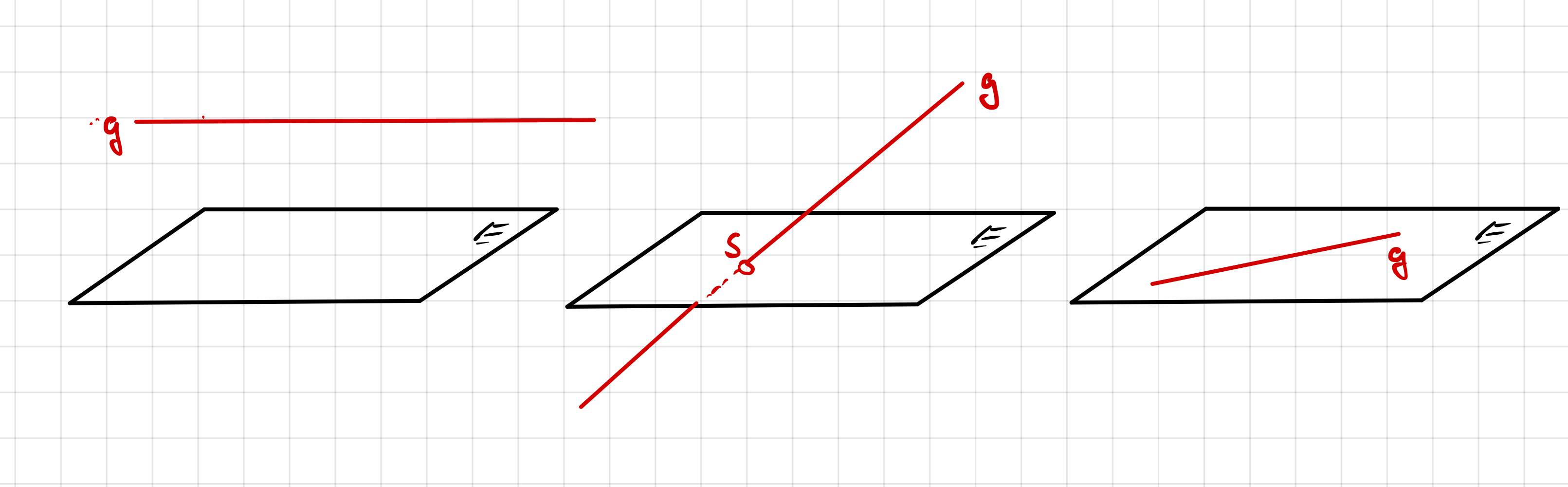
- keine Lösung
- kein gemeinsamer Punkt		 - genau eine Lösung
- ein Schnittpunkt S		 - unendlich viel Lösungen
- g verläuft in E
\(g ||| E\) \(g \cap E ={S}\) \(g \subset E\)

 

Unterscheidung in der Praxis

Gegeben ist die Gleichung einer Ebene  \(\small E: \space 2x_1-3x_2+6x_3-15=0\).

Im Folgenden untersuchen wir die Lage gegebenen Geraden gegenüber dieser Ebene E indem wir die Punktprobe mit dem allgemeinen Geradenpunkt durchführen und das Ergebnis der Gleichung geometrisch deuten:

 

\(\small g: \space \vec{X}=\left( \begin{array}{c} -2 \\ 3 \\ -4  \end{array}\right)  + k \cdot  \left( \begin{array}{c} -1 \\ 2 \\ -3  \end{array}\right)  \hspace{5mm} \Rightarrow \space\) Allg. Geradenpunkt: \(\small X(-2-k|3+2k|-4-3k)\)

Einsetzen von  \(\small X\) in KF(E): \(\small 2 \cdot (-2-k)-3 \cdot (3+2k)+6 \cdot (-4-3k)-15=0\)
  \(\small -4-2k-9-6k-24-18k-15=0\)
  \( \small -52-26k =0 \space \Rightarrow \space \color{red}{k=2}\)
  g und h schneiden sich im Punkt \(\small S(0|-1|2) \)

\(\small h: \space \vec{X}=\left( \begin{array}{c} 3 \\ -5 \\ -1  \end{array}\right)  + r \cdot  \left( \begin{array}{c} 0 \\ 2 \\ 1  \end{array}\right)  \hspace{5mm} \Rightarrow \space\) Allg. Geradenpunkt: \(\small X(3|-5+2r|-1+r)\)

Einsetzen von  \(\small X\) in KF(E): \(\small 2 \cdot 3-3 \cdot (-5+2r)+6 \cdot (-1+r)-15=0\)
  \(\small 6+15-6r-6+6r-15=0\)
  \( \small 0 =0 \)
  Unabhängig von r erhalten wir stets eine wahre Aussage!
Es gibt unendlich viele Lösungen: g verläuft in E

\(\small k: \space \vec{X}=\left( \begin{array}{c} 1 \\ -3 \\ 1  \end{array}\right)  + s \cdot  \left( \begin{array}{c} 3 \\ 4 \\ 1  \end{array}\right)  \hspace{5mm} \Rightarrow \space\) Allg. Geradenpunkt: \(\small X(1+3s|-3+4s|1+s)\)

Einsetzen von  \(\small X\) in KF(E): \(\small 2 \cdot (1+3s)-3 \cdot (-3+4s)+6 \cdot (1+s)-15=0\)
  \(\small 2+6s+9-12s+6+6s-15=0\)
  \( \small -16 =0 \)
  Es gibt keinen Wert r, der eine wahre Aussage liefert und daher keine Lösungen: g verläuft parallel zu E