4.5.1 Analyse der Lage zweier Ebenen

 

Zur Unterscheidung der gegenseitigen Lage zweier Ebenen haben wir je nach vorliegender Ebenenform verschiedene Ansätze zur Verfügung.

Standardmethode Normalenvektor

Wir lesen die jeweiligen Normalenvektor direkt aus der Normalen- oder Koordinatenform ab oder ermitteln diese(n) aus der Parameterform nach bekannten Techniken.

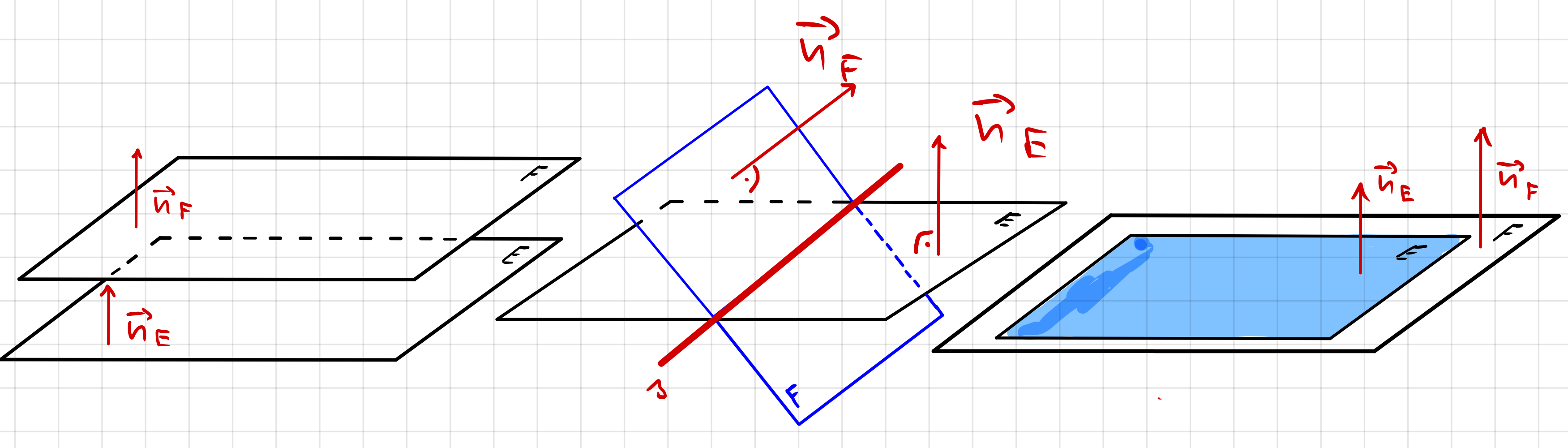
• 1. Fall:
  Sind die Normalenvektoren \(\small \vec{n_E}\)  und  \(\small \vec{n_F}\)  keine Vielfache voneinander, dann schneiden sich die Ebenen in einer gemeinsamen Schnittgeraden s.
   
• 2. Fall:
  Sind die Normalenvektoren  \(\small \vec{n_E}\)  und  \(\small \vec{n_F}\)   Vielfache voneinander, dann muss geprüft werden, ob ein Punkt der Ebene E in der Ebene F liegt, oder umgekehrt.
  - falls ja, dann sind die Ebenen identisch
  - falls nein, dann verlaufen die Ebenen echt parallel

 

Gleichsetzungs - oder Einsetzungsverfahren

Wir können uns ohne vorherige Analyse der gegenseitigen Lage mit Hilfe von Gleichsetzungsverfahren (Beide Ebenen in Parameterform!) oder Einsetzungsverfahren (Eine Koordinatenform und eine Parameterform!) sofort an die Berechnung der Schnittgeraden machen.

Wir kennen diese Arbeitsweise aus der Schnittpunktberechnung zwischen Gerade und Ebene.

Wieder müssen wir die Lösung der entsprechenden Gleichung bzw. des Gleichungssystems deuten:

• Erhalten wir einen mathematischen Widerspruch z.B. \(0 = -3\), dann wissen wir, dass keine Lösung existiert. Die Geraden haben keinen gemeinsamen Punkt und sind daher echt parallel.
• Erhalten wir unendlich viele Lösungen, dann sind die Ebenen identisch.
• Falls wir eine Geradengleichung als Lösung erhalten, dann haben wir die Schnittgerade der Ebenen bestimmt.

 

---