

Im Folgenden werden verschiedene Formen der Lagebeziehung mit ausgearbeiteten Lösungsansätzen vorgestellt, falls eine Ebene in Koordinatenform und die andere in Parameterform vorliegt. Dabei werden auch verschiedene Lösungsverfahren vorgestellt.
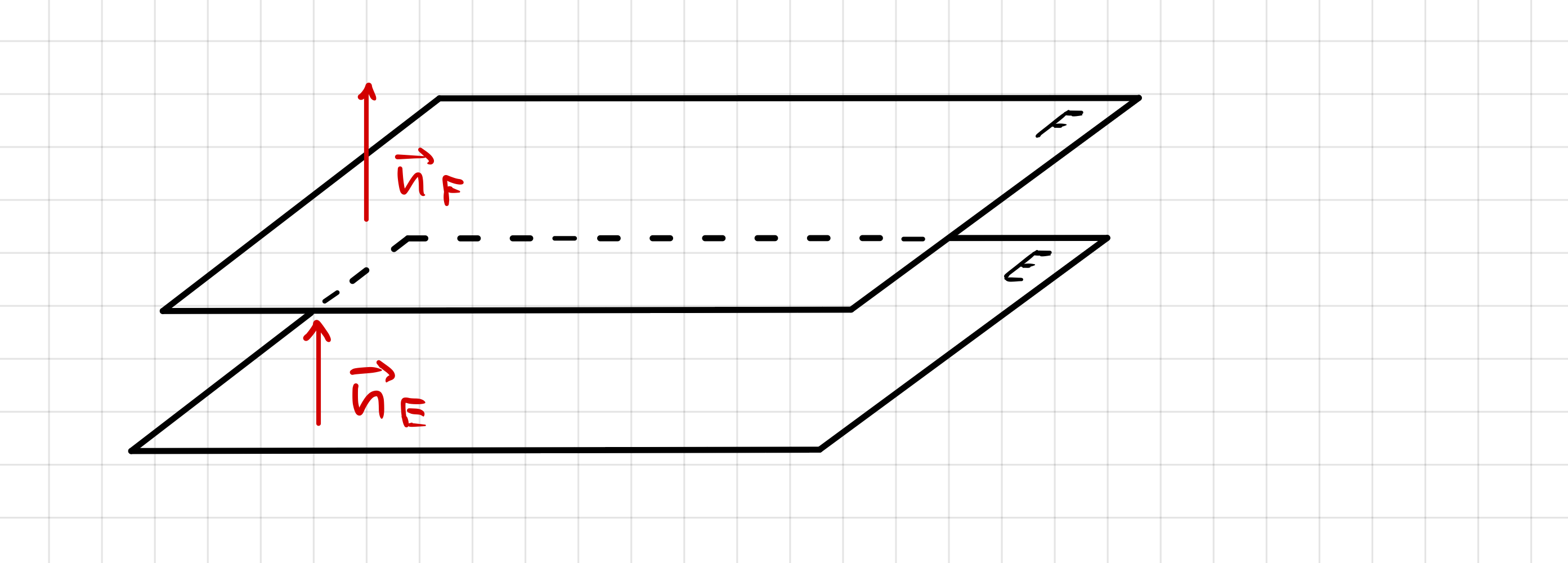
Bsp. 1: Die Ebenen sind echt parallel
| \(\small E : \hspace{6mm} 2x_1+4x_2+4x_3-5=0\) \(\small F: \space \vec{X}=\left( \begin{array}{c} 1 \\ 4 \\ -3 \end{array}\right) + \lambda \cdot \left( \begin{array}{c} 2 \\ -1 \\ 0 \end{array}\right) + \mu \cdot \left( \begin{array}{c} 0 \\ -1 \\ 1 \end{array}\right) \) |
 |
|
Für die Untersuchung der gegenseitigen Lage zweier Ebenen gibt es stets zwei Verfahren, die beide nach Analyse der Ergebnisse zum Ziel führen:
|
|
|
a)
Einsetzen von F in E: \(\space \small 2 \cdot (1+2\lambda) + 4 \cdot (4-\lambda-\mu)+ 4 \cdot(-3+\mu)-5=0\) \( \space \small 2+4 \lambda + 16 - 4\lambda-4\mu-12+4\mu-5=0 \) \( \space \small \hspace{70mm} 1 = 0 \hspace{10mm} \Rightarrow \space\) Die Ebenen sind echt parallel. |
|
|
b) Lage prüfen Normalenvektoren berechnen und
vergleichen: |
|
| Beide Lösungsverfahren zeigen durch den Widerspruch, dass es keine gemeinsamen Punkte gibt und die Ebenen echt parallel zueinander liegen! | |
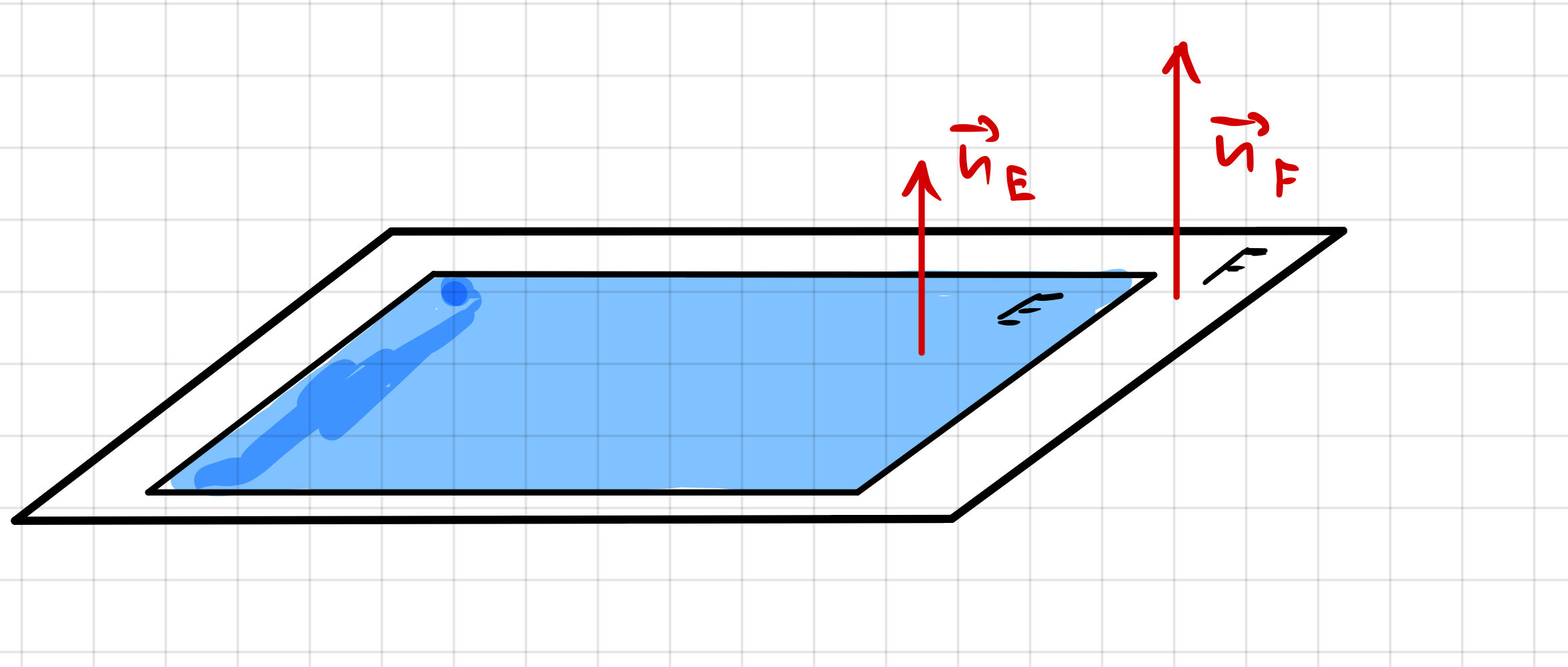
Bsp. 2: Die Ebenen sind identisch
| \(\small E : \hspace{6mm} 2x_1+4x_2+4x_3-6=0\) \(\small F: \space \vec{X}=\left( \begin{array}{c} 1 \\ 2 \\ -1 \end{array}\right) + \lambda \cdot \left( \begin{array}{c} 2 \\ -1 \\ 0 \end{array}\right) + \mu \cdot \left( \begin{array}{c} 0 \\ -1 \\ 1 \end{array}\right) \) |
 |
|
a)
Einsetzen von F in E: \(\space \small 2 \cdot (1+2\lambda) + 4 \cdot (2-\lambda-\mu)+ 4 \cdot(-1+\mu)-6=0\) \( \space \small 2+4 \lambda + 8 - 4\lambda-4\mu-4+4\mu-6=0 \) \( \space \small \hspace{65mm} 0 = 0 \hspace{10mm} \Rightarrow \space\) Die Ebenen sind identisch. |
|
|
b) Lage prüfen Normalenvektoren berechnen und
vergleichen: |
|
| Beide Lösungsverfahren zeigen, dass die jeweilige Gleichung für alle Werte von \(\lambda\) und \(\mu\) erfüllt weder und daher die Ebenen identsich sind! | |
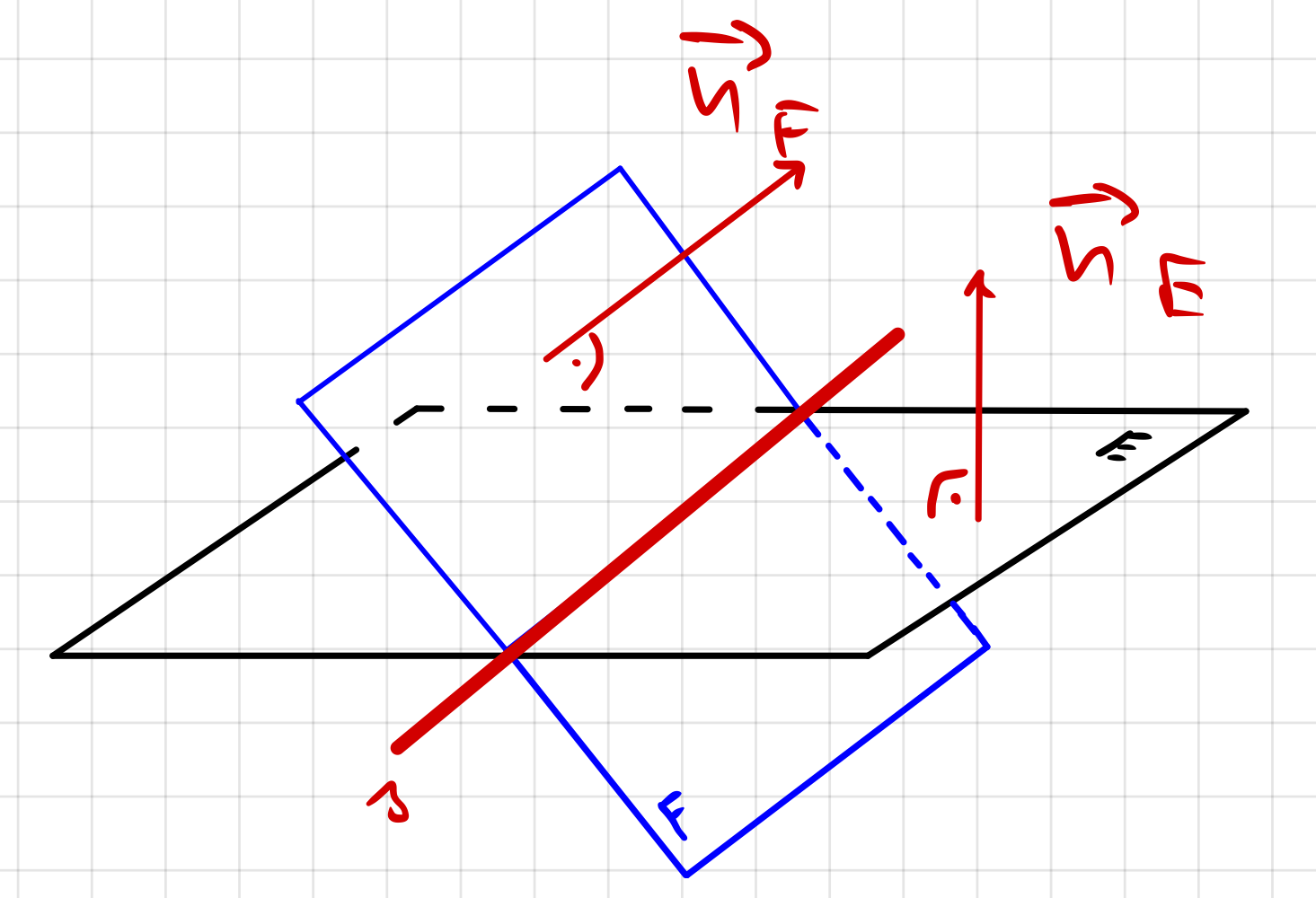
Bsp. 3: Die Ebenen schneiden sich
| \(\small E : \hspace{6mm} 2x_1+4x_2+4x_3+12=0\) \(\small F: \space \vec{X}=\left( \begin{array}{c} 0 \\ 2 \\ -1 \end{array}\right) + \lambda \cdot \left( \begin{array}{c} 1 \\ -1 \\ 0 \end{array}\right) + \mu \cdot \left( \begin{array}{c} 0 \\ 1 \\ -1 \end{array}\right) \) |
 |
|
a)
Einsetzen von F in E: \(\space \small 2 \cdot \lambda + 4 \cdot (2-\lambda+\mu)+ 4 \cdot(-1-2\mu)+12=0\) \( \space \small 2 \lambda + 8 - 4\lambda-4\mu-4+8\mu+16=0 \) \( \space \small \Rightarrow \space \lambda = -2\mu + 8 \) \( \space \small \Rightarrow \space\) \(\lambda\) lässt sich in Abhängigkeit von \(\mu\) berechnen. \( \space \small \Rightarrow \space\) Es existiert eine Schnittgerade! \( \space \small \Rightarrow \space\) Einsetzten von \(\lambda = -2\mu + 8 \) in die Ebene F liefert diese Schnittgerade \(s\). \(\small s: \space \vec{X}=\left( \begin{array}{c} 0 \\ 2 \\ -1 \end{array}\right) + (-2\mu+8) \cdot \left( \begin{array}{c} 1 \\ -1 \\ 0 \end{array}\right) + \mu \cdot \left( \begin{array}{c} 0 \\ 1 \\ -1 \end{array}\right) \) \(\small s: \space \vec{X}=\left( \begin{array}{c} 8 \\ -6 \\ -1 \end{array}\right) + \mu \cdot \left( \begin{array}{c} -2 \\ 3 \\ -1 \end{array}\right) \) |
|
|
b) Lage prüfen Normalenvektoren berechnen und vergleichen: \(\small \vec{n_F}=\left( \begin{array}{c} 2 \\ 4 \\ 4 \end{array}\right) \neq r \cdot \left( \begin{array}{c} 2 \\ 2 \\ 1 \end{array}\right) \) \(\hspace{10mm}\Rightarrow \space\) Die beiden Ebenen schneiden sich! \(\hspace{10mm}\Rightarrow \space\) Zur Berechnung der
Schnittgerade: Weiter mit Punkt a) |
|