Bild_Oben

4.5.5 Ausgearbeitete Beispiele zur Lagebeziehung

Im Folgenden werden verschiedene Formen der Lagebeziehung mit ausgearbeiteten Lösungsansätzen vorgestellt, falls beide Ebenen in Koordinatenform vorliegen. Dabei werden auch verschiedene Lösungsverfahren vorgestellt.

 

Beide Ebenen in Koordinatenform

 

Bsp. 1:  Die Ebenen sind echt parallel

\(\small E : \hspace{6mm} 2x_1-3x_2+x_3-6=0\)
\(\small F : \space -4x_1+6x_2-2x_3+2=0 \)
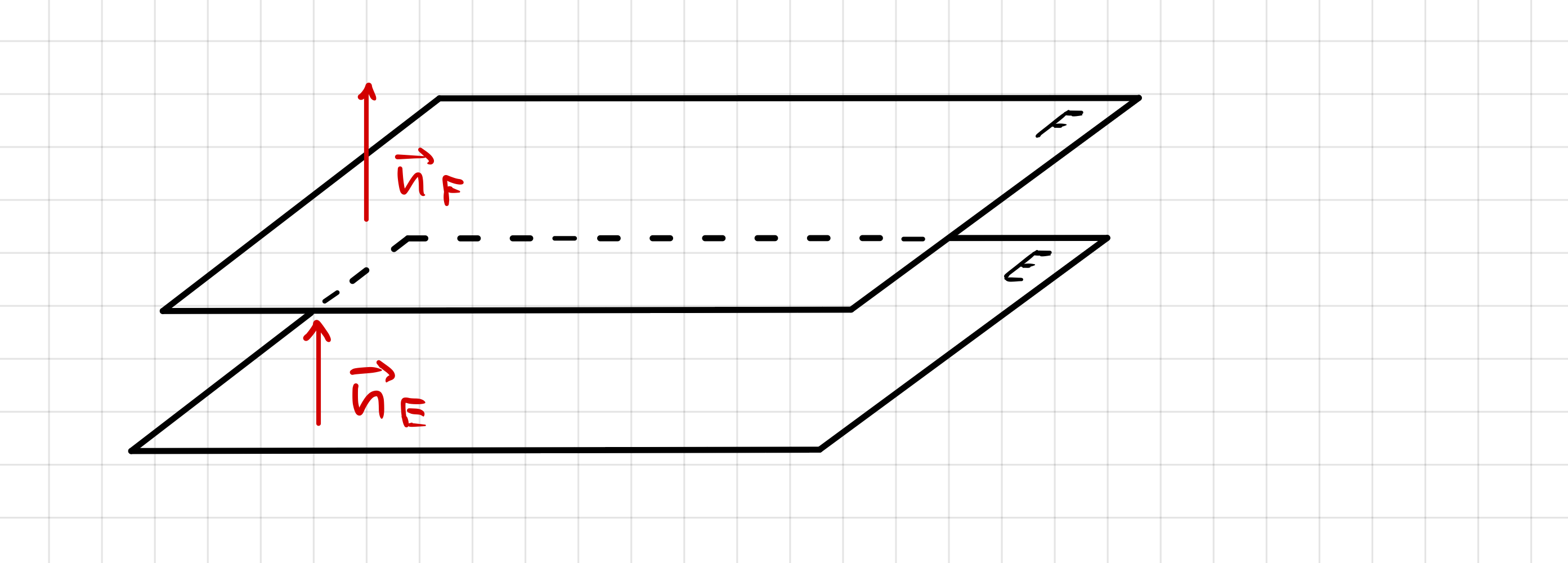Für die Richtungsvektoren gilt: \(\small \vec{n_F} = -2 \cdot \vec{n_E}\) ,   d.h. die Ebenen sind parallel.
Jedoch ist die Ebene F keine Vielfache der Ebene E. Multiplizieren wir die Ebene E mit \(\small -2\) dann erhalten wir  \(\small E : \space -4x_1+6x_2-2x_3+12=0\). Die Konstanten führen zum Widerspruch und wir können festhalten, dass beide Ebenen echt parallel verlaufen.

 

Bsp. 2:  Die Ebenen sind identisch

\(\small E : \hspace{6mm} 2x_1-3x_2+x_3-6=0\)
\(\small F : \space -4x_1+6x_2-2x_3+12=0 \)
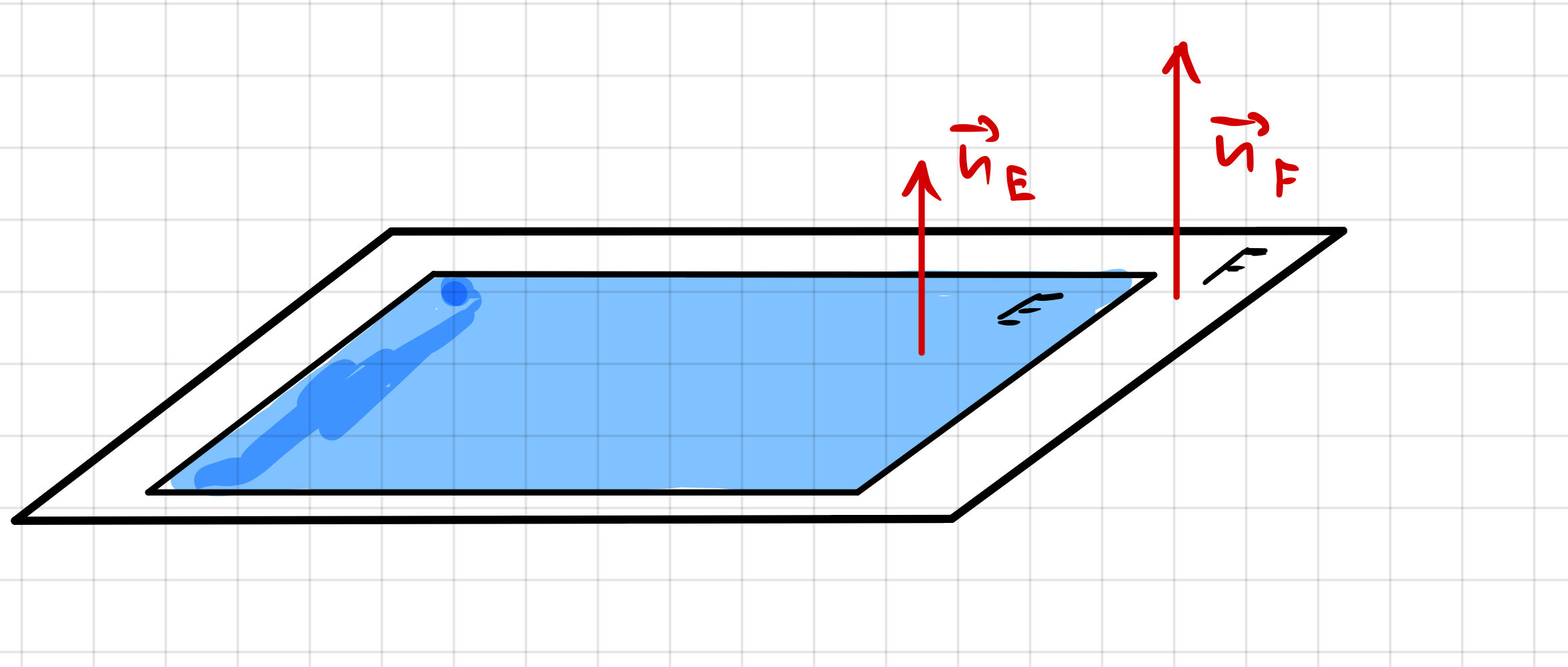Die Ebene F eine Vielfache der Ebene E. Multiplizieren wir die Gleichung E mit \(\small -2\),  dann erhalten wir  \(\small E : \space -4x_1+6x_2-2x_3+12=0\), also die Gleichung der Ebene F. Beide Ebenen sind somit  identisch.

 

Bsp. 3:  Die Ebenen schneiden sich

\(\small E : \hspace{2mm} x_1+x_2-2x_3+5=0\)
\(\small F : \space 2x_1-x_2+x_3-4=0 \)
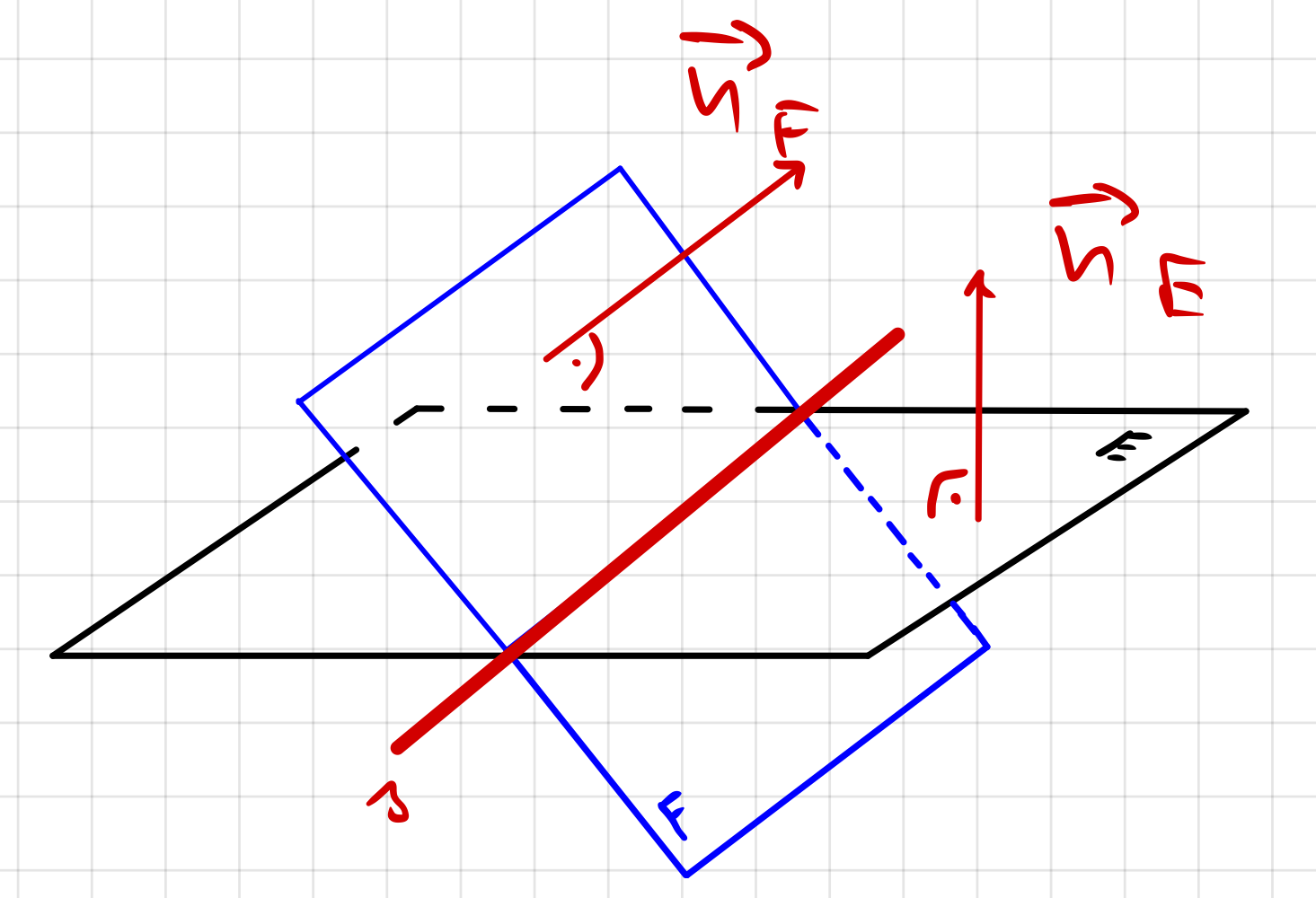Die Richtungsvektoren sind keine Vielfache voneinander. Die Ebenen scheiden sich in einer gemeinsamen Schnittgeraden \(s\).

Methode: Gleichungssystem:
Die Koordinatenformen beider Ebenengleichungen können als Gleichungen eines unterbestimmten Gleichungssystems aufgefasst werden. Die Lösung des Gleichungssystems sind alle Punkte, die beide Gleichungen erfüllen, also die gesuchte Schnittgerade \(s\).
 
I)  \(\small \hspace{2mm} x_1+x_2-2x_3+5=0\)
II) \(\small \hspace{2mm} 2x_1-x_2+x_3-4=0 \)
 		  
I) \(\small \hspace{12mm} x_2+x_1-2x_3+5=0 \)
I) + II)  \(\small \hspace{12mm} 3x_1-x_3+1=0\)
 
\(\Rightarrow \space x_3=3x_1+1\)
\(x_3\) in I) einsetzen:
\(\small x_2+x_1-6x_1-2+5=0\)
 
\(\Rightarrow \space x_2=5x_1-3\)
 
-> \(x_2\) und \(x_3\) sind durch \(x_1\) darstellbar.
-> eine Koordinate ist frei wählbar
\(\Rightarrow \space x_1=\lambda\)
   
Schnittgerade:   \(\small s: \space \vec{X}=\left( \begin{array}{c} x_1 \\ x_2 \\ x_3  \end{array}\right)=\left( \begin{array}{c} 0+ \lambda \\ -3+5 \lambda \\ 1+3 \lambda  \end{array}\right)  =\left( \begin{array}{c} 0 \\ -3 \\ 1  \end{array}\right)  + \lambda \cdot  \left( \begin{array}{c} 1 \\ 5 \\ 3  \end{array}\right) \)

 

 

Kurzanleitung:
  • Ebenengleichungen bilden ein unterbestimmtes Gleichungssystem
  • mit zwei Gleichungen und drei Unbekannte, die "Lösungskoordinaten".
  • Zur Lösung kann einen beliebige Variable frei gewählt werden.
  • Zwei Koordinaten werden also in Abhängigkeit der freien berechnet.
    Hier: \( \small x_1=\lambda \)
  • Alle "Lösungspunkte" liegen auf der Schnittgeraden \(s\).

 

 

Bsp. 4:  Die Ebenen schneiden sich

\(\small E : \hspace{2mm} 3x_1-4x_2-x_3-4=0\)
\(\small F : \space 3x_1-3x_2+x_3-3=0 \)
Die Richtungsvektoren sind keine Vielfache voneinander. Die Ebenen scheiden sich in einer gemeinsamen Schnittgeraden \(s\).

Methode: Gerade durch Richtungsvektor und Aufpunkt
Die Schnittgerade \(s\) liegt in beiden Ebenen und daher muss deren Richtungsvektor \(\vec{u_s}\) senkrecht zu den Normalenvektoren beider Ebenen verlaufen:

\( \vec{u_s} = \vec{n_E} \times \vec{n_F}=\small \left( \begin{array}{c} 3 \\ -4 \\ -1  \end{array}\right) \times \left( \begin{array}{c} 3 \\ -3 \\ 1 \end{array}\right)=\left( \begin{array}{c} -7 \\ -6 \\ 3  \end{array}\right)\)


Bestimme noch einen gemeinsamen Punkt der Ebenen über das Gleichungssystem:

I)  \(\small \hspace{2mm} 3x_1-4x_2-x_3-4=0\)
II) \(\small \hspace{2mm} 3x_1-3x_2+x_3-3=0 \)

I) \(\small \hspace{12mm} 3x_1-4x_2-x_3-4=0 \)
I) - II)  \(\small \hspace{12mm} -x_2-2x_3-1=0\)  (IV)

\(\Rightarrow \small \space A(x_1|-3|1)\)    löst die Gleichung (IV)

\(\Rightarrow \space \)mit Gleichung I) oder II) erhalten wir  \(x_1=-\frac{7}{3}\) und:   \(A(-\frac{7}{3}|-3|1)\)
   
Schnittgerade:   \(\small s: \space \vec{X}=\vec{A}+\lambda \vec{u_s}=\left( \begin{array}{c} -\frac{7}{3} \\ -3 \\ 1  \end{array}\right) + \lambda \cdot  \left( \begin{array}{c} -7 \\ -6 \\ 3  \end{array}\right) \)

 

 

Bsp. 5:  Die Ebenen schneiden sich

\(\small E : \hspace{2mm} 3x_1-4x_2-x_3-4=0\)
\(\small F : \space 3x_1-3x_2+x_3-3=0 \)
Die Richtungsvektoren sind keine Vielfache voneinander. Die Ebenen scheiden sich in einer gemeinsamen Schnittgeraden \(s\).

Methode: Gerade durch zwei gemeinsame Punkte
Die Schnittgerade \(s\) liegt in beiden Ebenen und daher kann die Gleichung durch zwei gemeinsame Punkte der Ebenen E und F aufgestellt werden:


Bestimme die gemeinsamen Punkte der Ebenen über das Gleichungssystem:

I)  \(\small \hspace{2mm} 3x_1-4x_2-x_3-4=0\)
II) \(\small \hspace{2mm} 3x_1-3x_2+x_3-3=0 \)

I) \(\small \hspace{12mm} 3x_1-4x_2-x_3-4=0 \)
I) - II)  \(\small \hspace{12mm} -x_2-2x_3-1=0\)  (IV)

\(\Rightarrow \small \space A(x_1|-3|1)\)    löst die Gleichung (IV)
\(\Rightarrow \space \)mit Gleichung I) oder II) erhalten wir  \(x_1=-\frac{7}{3}\)  und:   \(A(-\frac{7}{3}|-3|1)\)

\(\Rightarrow \small \space B(x_1|-1|0)\)    löst die Gleichung (IV)
\(\Rightarrow \space \)mit Gleichung I) oder II) erhalten wir  \(x_1=0\)    und:     \(B(0|-1|0)\)
 
Schnittgerade   \(\small s: \space \vec{X}=\vec{A}+\lambda \cdot \vec{AB}=\left( \begin{array}{c} -\frac{7}{3} \\ -3 \\ 1  \end{array}\right) + \lambda \cdot  \left( \begin{array}{c} \frac{7}{3} \\ 2 \\ -1  \end{array}\right) \)