1.5.2 Rechengesetze der Vektoraddition

Für das Addieren von Vektoren gelten die gleichen Gesetze wie für das Addieren von beliebigen Zahlen:

 

Kommutativität der Vektoraddition

Zwei Vektoren \(\vec{u}\) und \(\vec{v}\) repräsentieren zwei Verschiebungen im \(R^3\). Aufgrund der bisherigen Betrachtungen ist schnell nachvollziehbar, dass die Reihenfolge der Verschiebungen für die daraus resultierende Verschiebung egal ist.

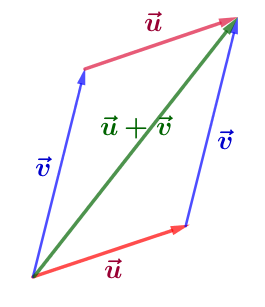
Anhand der Rechnung und der Grafik ist der Nachweis der Kommutativität der Vektoraddition mit den oben verwendeten Vektoren \(\vec{u}\) und \(\vec{v}\) schnell gezeigt:

 

\( \vec{u}+\vec{v}= \left( \begin{array}{c} 2 \\ 4 \\ 1  \end{array}\right) + \left( \begin{array}{c} -5 \\ 2 \\ 3 \end{array} \right)  = \left( \begin{array}{c} 2+(-5) \\ 4+2 \\ 1+3 \end{array} \right)  = \left( \begin{array}{c} -3 \\ 6 \\ 4 \end{array} \right) \)   \( \vec{v}+\vec{u}= \left( \begin{array}{c} -5 \\ 2 \\ 3  \end{array}\right) + \left( \begin{array}{c} 2 \\ 4 \\ 1 \end{array} \right)  = \left( \begin{array}{c} -5+2 \\ 2+4 \\ 3+1 \end{array} \right)  = \left( \begin{array}{c} -3 \\ 6 \\ 4 \end{array} \right) \)

 

Ergebnis: Egal in welcher Reihenfolge wir die beiden Vektoren \( \vec{u}\) und \( \vec{v} \) addieren bzw. die beiden Verschiebungen \( \vec{u}\) und \( \vec{v} \) ausführen, wir erhalten stets denselben Summenvektor bzw. dieselbe Gesamtverschiebung \( \vec{u} + \vec{v} \). Die Vektoraddtion ist also stets kommutativ (vertauschbar) und es gilt stets: \[ \vec{u} + \vec{v}= \vec{v} + \vec{u}\]

 

Assoziativgesetz der Addition

Wie für die Addition von mehr als zwei Zahlen spielt auch die Reihenfolge der entsprechenden Ausführung bei der Addition von Vektoren keine Rolle. Wir können ebenfalls das Assoziativgesetz der Vektoraddition anwenden und Klammern beliebig setzen.

 

Beim Rechnen mit  Vektoren gilt stets das Assoziativgesetzt der Vektoraddition:     \[ (\vec{u} + \vec{v})+\vec{w}= \vec{u} +( \vec{v}+\vec{w})\]

 

 

---