1.5.3 Multiplikation eines Vektors mit einer Zahl

 

Die Multiplikation eines Vektors mit einer beliebigen Zahl können wir mit der Vervielfachung eines Vektors umschreiben.

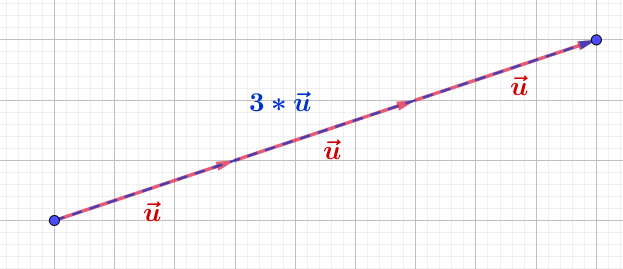
Führen wir dreimal hintereinander die Verschiebung mit dem Vektor \( \vec{u} \) durch, dann können wir diesen Operation folgendermaßen formulieren:

\[ \vec{u}+ \vec{u} + \vec{u} = 3 \cdot \vec{u} \]

Der Vektor \( 3\vec{u} \) ist dreimal so lang wie der Vektor \(\vec{u}\) und zeigt in die gleiche Richtung wie der Vektor \(\vec{u}\).

 

Skalare Multiplikation (S-Multiplikation)

Zahlen werden zur Unterscheidung von Vektoren auch als Skalare bezeichnet und so spricht man bei der Multiplikation eines Vektors mit einer Zahl auch von der skalaren Multiplikation (S-Multiplikation).

 

Definition: Die Multiplikation eines Vektors   \( \vec{v} = \left( \begin{array}{c} v_1 \\ v_2 \\ v_3 \end{array} \right) \)  mit \(k \in R\)  wird skalare Multiplikation genannt und diese ist folgendermaßen definiert:  \[ k \cdot \vec{v} = k \cdot \left( \begin{array}{c} v_1 \\ v_2 \\ v_3 \end{array} \right)= \left( \begin{array}{c} k \cdot v_1 \\ k \cdot v_2 \\ k \cdot v_3 \end{array} \right) \]   Die skalare Multiplikation hat folgende Eigenschaften: Der Vektor  \(k \cdot \vec{v}\)  ist  \(|k|-\) mal so lang wie der Vektor \(\vec{v}\) und stets parallel zum Vektor \(\vec{v}\). Falls \(k>0\), dann ist der Vektor \(k \cdot \vec{v}\)  gleich gerichtet zum Vektor  \(\vec{v}\). Falls \(k<0\), dann ist der Vektor \(k \cdot \vec{v}\)  entgegengesetzt gerichtet zum Vektor  \(\vec{v}\).

 

Besonderheiten:

• Die Multiplikation eines Vektors \(\vec{v}\) mit der Zahl \(0\) erzeugt den sogenannten Nullvektor und nicht die Zahl Null

\(0 \cdot \vec{v}=\vec{0}\)

  

• Durch Multiplikation eines Vektors  \( \vec{v}\)  mit \(-1\) erhalten
  wir den sogenannten Gegenvektor  \( -\vec{v}\)   zu   \( \vec{v}\).

\(-1 \cdot  \vec{v}=-\vec{v} \) 

 

 

 

---